Výpočet obsahu plochy ohraničeného mnohostranným (polygonálním) útvarem, který vznikne pospojováním bodů v mřížových bodech lze provést pomocí Pickova vzorce. Georg Pick byl rakouský matematik, který přijal v roce 1880 na Karlo-Ferdinandově univerzitě v Praze místo pomocného asistenta  významného fyzika Ernsta Macha. Pick byl blízkým přítelem Alberta Einsteina a v roce 1911 jej pozval, aby  působil na německé části Karlovy univerzity v Praze. Pick se zabýval především geometrií a proslavil se v geometrii mřížových bodů vzorcem, který po něm dostal jméno.

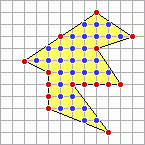
Pokud chceme určit obsah útvaru ohraničeného lomenou čarou na mřížce bodů, musíme zjistit počet bodů na hranici útvaru (červené body: b = 15) a počet vnitřních bodů v útvaru (modré : c = 31). Pickův vzorec má podobu:

                                                            S = c + b/2 –1

Pro náš obrázek vychází: S = 31 + 15/2 –1 = 37,5 plošných jednotek

Pickův vzorec můžeme použít pro libovolný útvar, který vznikne pospojováním diskrétních bodů s celočíselnými souřadnicemi. Jedinou podmínkou zůstává, že hranice nesmí protínat sama sebe.